地球的引力势能公式及其应用
地球的引力势能公式及其应用
引力势能公式的推导
处在地球引力场中的物体在靠近地球或远离地球时,万有引力会对物体做功,从而引起物体引力势能的变化,且引力做多少功,物体的引力势能就会减小多少-----功能关系。

如图所示,设地球的质量为M,物体的质量为m,物体与地球之间的距离为r。现将物体从r处移到离地球无穷远处,地球引力对物体做了多少功呢?
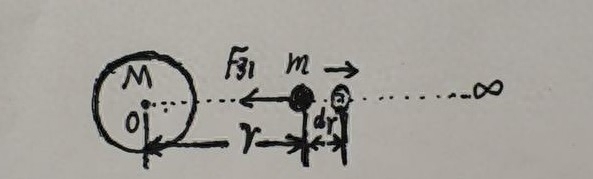
当物体移动很小的距离dr时,万有引力对物体做的功dW为:
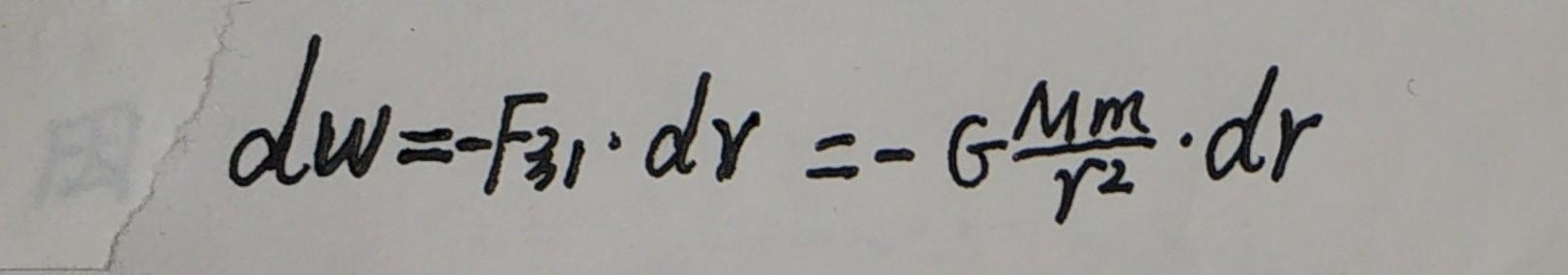
将这些功累积起来,就可得到地球引力对物体做的功W为:
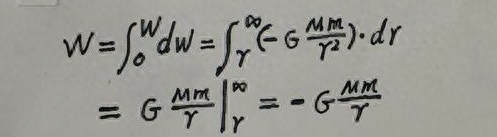
规定物体在无穷远处的引力势能为零,即Ep∞=0,结合功能关系可以的到:
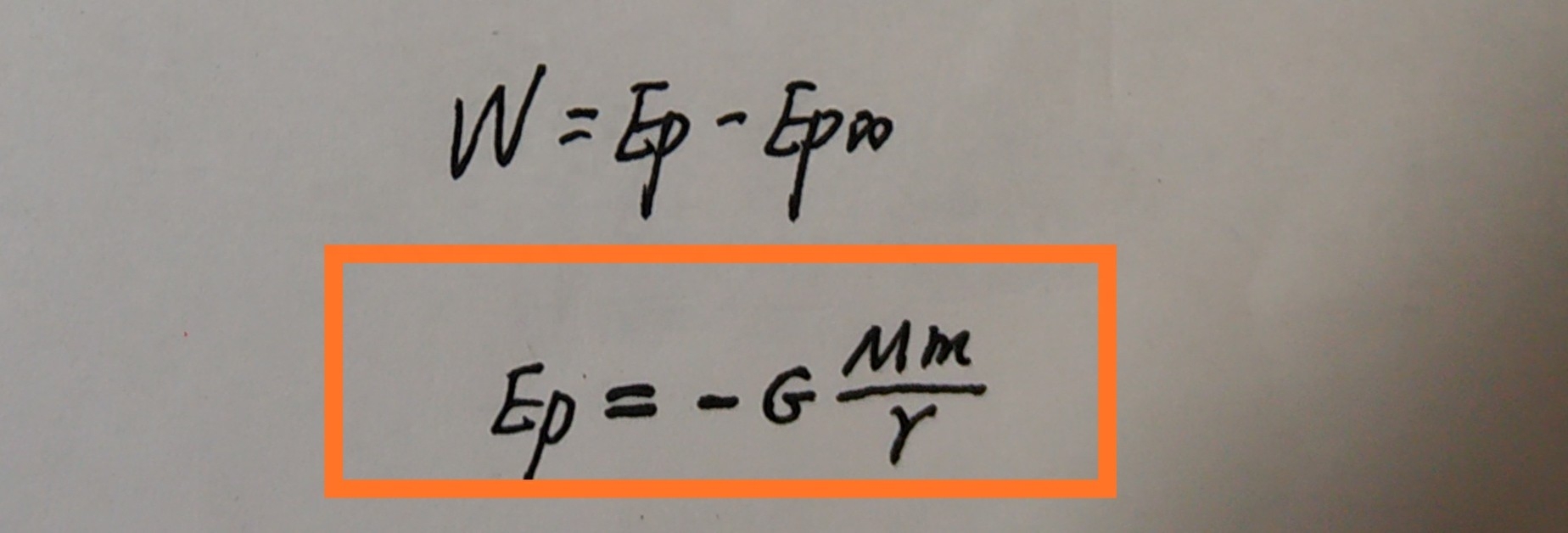
以上即为物体在距离地球r的地方引力势能的表达式。
引力势能公式的应用
1.推导发射航天器的第二宇宙速度
当航天器的发射速度超过一定值时,它就可以摆脱地球引力的束缚,飞离地球进入环绕太阳运行的轨道。这个脱离地球引力的最小发射速度就是第二宇宙速度。

设地球的半径为R,当航天器的发射速度为v时,航天器恰好能脱离地球的吸引,即到达(相对地球)无穷远处。该过程航天器的发射动能转化为引力势能,根据机械能守恒定律得:
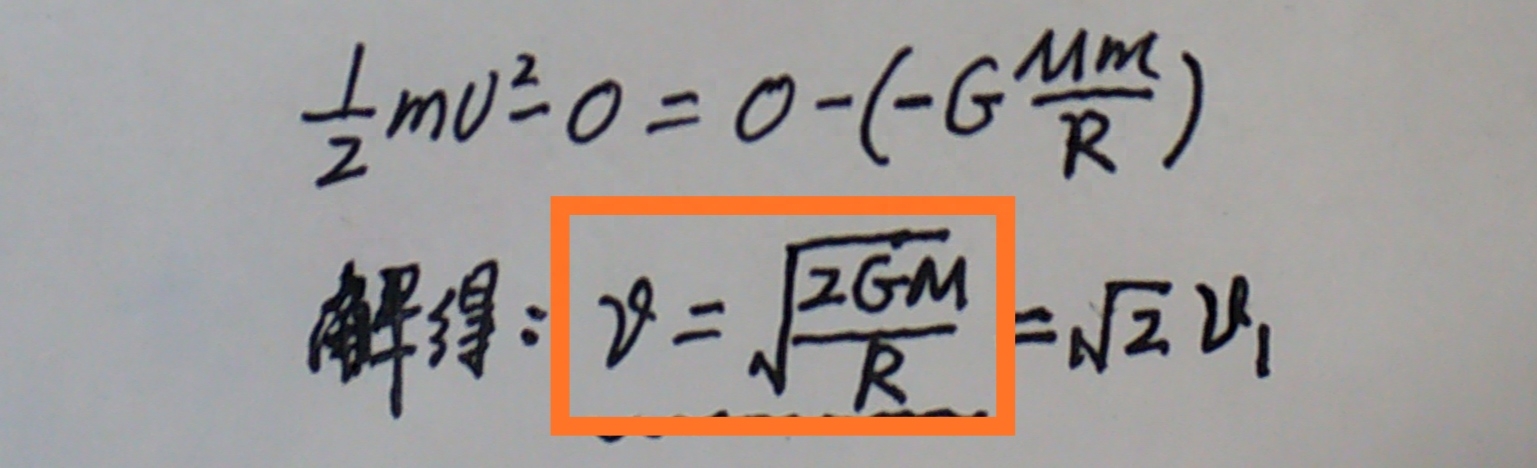
从以上结果可以看出,第二宇宙速度是第一宇宙速度的根2倍,约等于11.2km/s。
2.计算卫星变轨的机械能变化
如图所示为卫星变轨的简单示意图,我们知道,卫星从一个低轨道1‘’升迁‘’至高轨道3至少要经过两次点火加速,所以卫星运行的轨道越高,机械能越大。卫星在变轨过程中至少要补充多少机械能呢?
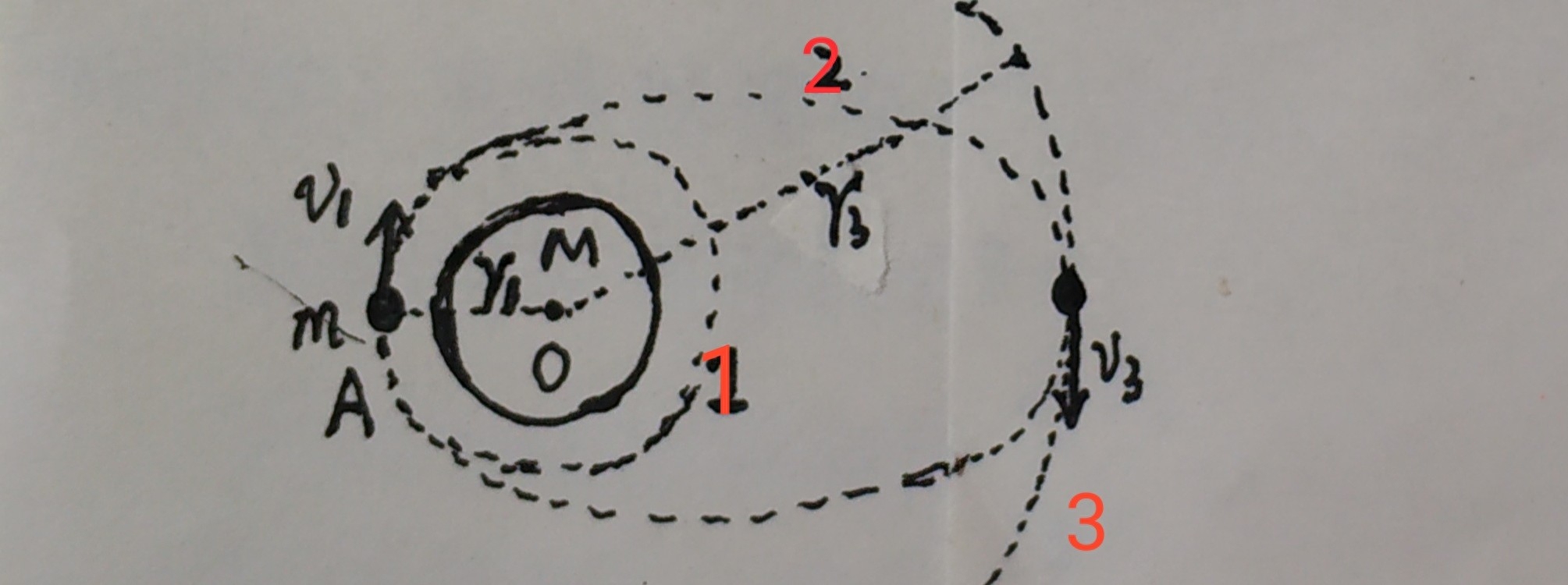
卫星在轨道1和轨道3上做圆周运动时,都是由万有引力提供向心力,根据牛顿第二定律可确定卫星在两个轨道上运行时的动能如下:
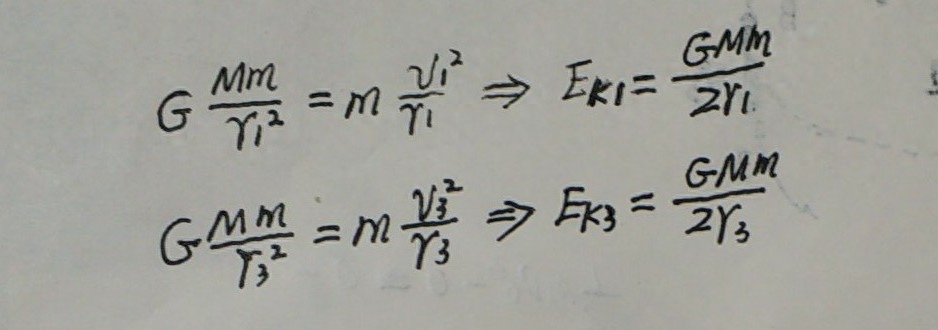
结合引力势能公式可确定卫星在两个轨道上运行时的机械能分别为:
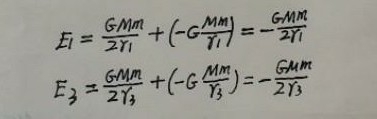
所以卫星在变轨过程中至少要补充的机械能为:
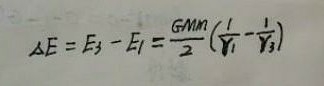
-

- 当兵对于学历有什么要求,你知道吗?
-
2023-12-22 08:22:33
-

- 678文化街,伦教最值得品的文化街道
-
2023-12-22 08:20:27
-

- 46岁皮蓬前妻被球哥等人追求,为何最美NBA记者艾比无人追求?
-
2023-12-22 08:18:21
-

- 「怪猎冰原」PC版大感谢祭活动任务详解
-
2023-12-22 08:16:16
-

- “叫板”只是挑衅和“battle”的意思?你可知它真正来源于哪里?
-
2023-12-22 08:14:10
-

- 如何申请网站 ?网站域名地址怎样和IP地址绑定?
-
2023-12-22 06:40:01
-

- 肉泡在水里解冻正确吗 给肉解冻,最忌直接用水泡,教你正确解冻方法
-
2023-12-22 06:37:56
-

- 家用制氧机好吗有辐射吗(都在吹嘘家用分子筛制氧机的好,难道它就没有缺点吗
-
2023-12-22 06:35:51
-

- 个人简历封面制作教程(可爱的简历封面制作,这一款你值得试一试)
-
2023-12-22 06:33:46
-

- 粉色玫瑰花语是什么(粉玫瑰花语,11朵-99朵粉玫瑰分别代表什么?)
-
2023-12-22 06:31:42
-

- 垂盆草的功效与作用(既可治疱疹 又可治肝炎)
-
2023-12-22 06:29:37
-

- 煮玉米的做法教程(煮玉米,记住正确做法教程,才会更甜更香更软糯,不要只会
-
2023-12-22 06:27:32
-

- 养花妙用陶粒,扦插、水培都能用,人人都叫你绿手指
-
2023-12-22 06:25:27
-

- 喜庆的歌曲有哪些好听(盘点适合过年听的十大喜庆歌曲,你听过几首?)
-
2023-12-22 06:23:22
-

- 如何钓黑鱼 我钓黑鱼的4种方法,曾经一次钓了8条大家伙
-
2023-12-22 06:21:17
-
- 瑞丽在哪个省的哪个市(云南省瑞丽市有21万人口,这里三面环缅甸,有南畹河与
-
2023-12-21 16:58:33
-

- 帕拉梅拉怎么样来的(追溯保时捷帕拉梅拉的前世今生,设计理念源于生活,却又
-
2023-12-21 16:56:28
-

- 嫁给什么样的男生最幸福(嫁给这四种男人,婚姻更容易幸福,你嫁对了吗?)
-
2023-12-21 16:54:22
-

- 孩子厌学怎么办 有什么方法 孩子厌学了,怎么办?
-
2023-12-21 16:52:16
-

- 吃葡萄的好处(葡萄被誉为“美女的保护果”!常吃有哪些特殊的好处?)
-
2023-12-21 16:50:10



 云南本地人为什么不会被骗到缅甸(看看真实的缅北)
云南本地人为什么不会被骗到缅甸(看看真实的缅北) 中国一线男装10大品牌(盘点国内十大知名男装品牌排行榜)
中国一线男装10大品牌(盘点国内十大知名男装品牌排行榜)