逐差法公式的推导及应用(数字推理之逐差法)
逐差法公式的推导及应用(数字推理之逐差法)
2020年已经过去,新的篇章即将开始,而2021年各类招考也拉开序幕,随着各省省考的逐步推进,事业单位的备考也可以提上日程,而安徽事业单位笔试有别于省考笔试的一种题型就是数字推理。想要解决数字推理这一题型,那么就需要进行大量的练习,并且掌握一定的方法,而逐差法就是数字推理诸多方法中的一种。接下来,为广大考生总结了一些逐差法的基本应用,希望能给大家带来一些帮助!
一、含义:
指后项对前项依次作差,观察得到差的特点,再对得到的差进行分情况讨论。
二、常见应用
1.数列基本单调,从大数字看变化幅度不大(2倍左右);
2.数列中有若干负数,排列没有规律;
3.没有特殊办法时,强行逐次差寻找规律;
三、操作方法
1.逐差,随时关注差和基本数列的联系,一级差无特点时再逐一级差。
【例题1】 8,2,-2,-4,-4,()
A.-3 B.2 C.3 D.-2
【答案】D。
【中公解析】作一级差得:- 6,-4,-2,0,(2),所求为:-4+2=-2。所以本题选择D项。
【例题2】1.1, 2.1, 0.1, 4.1, -0.9, ( )
A.4 B.6.1 C.-4.1 D.5.1
【答案】B。
【中公解析】作一级差得:1, -2, 4, -5, (), 有负数没有其它规律,再作二级差得:-3, 6, -9,(12),绝对值加3,正负间隔。所以本题选择B项。
2.如果,二级差也无特点,则先将其放在一边,将一级差斜向代入原数列构造网络。
【例题3】 0,4,16,48,128,()
A.280 B.320 C.350 D.420
【答案】B。
【中公解析】作一级差得:4,12,32,80,斜向上构造网络为4倍关系,所求为80×4=320。所以本题选择B项。
3.如果无法构造网络,则需要对二级差“一逐到底”。随时结合差和倍数的大胆猜测。
【例题4】 4,1,0,2,10,29,66,()
A.101 B.116 C.125 D.130
【答案】D。
【中公解析】作一级差得:-3,-1,2,8,19,37,(64)没发现规律,作二级差得:2,3,6,11,18,(27)无规律,作三级差1,3,5,7,(9),为奇数列,所以推出18+9=27,27+37=64,64+66=130。所以本题选择D项。
通过以上内容的展示,希望广大考生能够熟悉题型特征,将逐差法学以致用,领悟到位。建议广大考生在平常做题过程中多加总结和练习,在平常进行思路的拓展,多加思考和积累,才能在考试的时候更加灵活的解决问题!
-

- 这才是板栗煲鸡的正宗做法,汤汁清甜又滋补,秋天喝很好
-
2024-01-02 10:33:03
-

- 长生草属的习性(多肉植物中的长生草属)
-
2024-01-02 10:30:57
-

- 如何开椰子? 看完这一篇,开椰子,取椰肉,做椰子鸡全学会了
-
2024-01-02 07:41:32
-

- 白雪公主出自哪本童话书(《白雪公主》的故事出自格林童话,它的原型故事是什
-
2024-01-02 07:39:27
-
- 玉镯最简单的鉴定方法 真假
-
2024-01-02 07:37:22
-
- 湿疣治疗 尖锐湿疣常用治疗方法优缺点汇总
-
2024-01-02 07:35:17
-
- 关元准确位置图和作用 按摩关元、命门穴化解“宫寒”!
-
2024-01-02 07:33:12
-

- 章鱼血是什么颜色的(章鱼的血是蓝色的 是外星人后裔?)
-
2024-01-02 07:31:07
-

- 英语是学会的不是教会的——学好英语的五条建议
-
2024-01-02 07:29:02
-
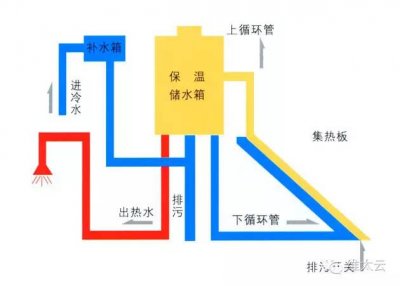
- 太阳能热水器工作原理图解(太阳能热水器安装示意图及工作原理图)
-
2024-01-02 07:26:57
-

- 什么时候出梅雨(2022年梅雨季节是什么时间?具体几号入梅?最新入梅出梅时间
-
2024-01-02 07:24:52
-

- 男人右眼跳是财还是灾预示着什么(“左眼跳财,右眼跳灾”,有科学依据吗?眼
-
2024-01-02 07:22:47
-
- 天津李四通过nzbz粉丝解散所有群
-
2024-01-01 04:14:38
-
- 如何辨别菠萝蜜的生熟?
-
2024-01-01 04:12:32
-
- 护照办理何时开放
-
2024-01-01 04:10:27
-

- 细数詹姆斯穿过24种不同配色的LeBron 15,你会喜欢哪双?
-
2024-01-01 04:08:21
-

- 墨西哥门将神级扑救 墨西哥队0比0平波兰队
-
2024-01-01 04:06:15
-

- 「毒品知识」什么是毒品?
-
2024-01-01 04:04:09
-

- “脐橙之乡”在哪里?
-
2024-01-01 04:02:03
-

- 韩国女模特韩惠珍最新时装杂志写真曝光
-
2024-01-01 03:59:58



 云南本地人为什么不会被骗到缅甸(看看真实的缅北)
云南本地人为什么不会被骗到缅甸(看看真实的缅北) 中国一线男装10大品牌(盘点国内十大知名男装品牌排行榜)
中国一线男装10大品牌(盘点国内十大知名男装品牌排行榜)